Suggestion: in lecture "Overfit-generalization-underfit" change orientation of histogram

M2. Selecting the best model
#1

Hi,
in entry n°5 you build a histogram to compare tain and test error. You wanted to show that train errors ~ 0 and test errors are significantly larger but you putted the “mean absolute errors” on x-axis. On charts most people look at y axis to compare data so I think it should be clearer at first view to change orientation of the chart to read the values you want to emphasize on the y-axis:

import matplotlib.pyplot as plt

scores.plot.hist(bins=50, edgecolor="black", orientation='horizontal')
plt.ylabel("Mean absolute error")
handles, labels = plt.gca().get_legend_handles_labels()
order =[1,0]
plt.legend([handles[idx] for idx in order],[labels[idx] for idx in order])
_ = plt.title("Train and test errors distribution via cross-validation")

image

#2

I personally find it weird to represent an histogram rotated. His is not super usual.

1 Like
#3

I agree that kind of representation is not common.
But I think it s counterintuitive to read the result on x axis if you keep histograms as you choose to draw.
Since you are not using at all the ‘frequency’ values in your conclusions why go for a histogram?
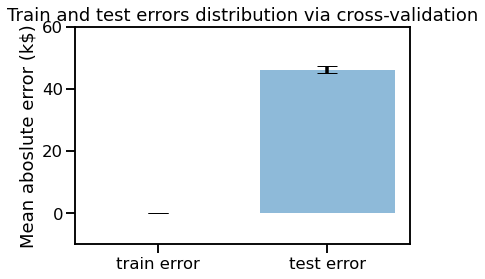
You could obtain a better visualisation of the difference between train and test errors in drawing a box plot or a bar plot:

import matplotlib.pyplot as plt
scores.plot.box()
plt.ylabel("Mean absolute error k$")
_ = plt.title("Train and test errors distribution via cross-validation")

image

train_error_mean = scores['train error'].mean()
test_error_mean = scores['test error'].mean()
train_error_std = scores['train error'].std()
test_error_std = scores['test error'].std()
x_labels = list(scores.columns)
x_pos = np.arange(len(x_labels))
CTEs = [train_error_mean, test_error_mean]
stds = [train_error_std, test_error_std]
fig, ax = plt.subplots()
ax.bar(x_pos, CTEs, yerr=stds, align='center', alpha=0.5, ecolor='black', capsize=10)
ax.set_ylabel('Mean aboslute error (k$)')
ax.set_xticks(x_pos)
ax.set_xticklabels(x_labels)
ax.set_title("Train and test errors distribution via cross-validation")

plt.ylim(ymin = -10, ymax = 60)
plt.show()

image

I remember that when i was still a student (a long time ago) the director of my lab was used to say that a figure should give all the informations needed without to have to read the commentaries below. When I saw your figures, before reading the conclusions i thought frequencies of the 2 distributions were important somehow since they were the values on y axis, the axis where you normaly the important results ;).

#4

I think most people reading an histogram find it natural to have (absolute or relative) frequency on the y-axis. Swapping the axis would be even more confusing.

But we could use a box-plot instead of histograms to summarize the difference between train and test scores measured on different CV iterations.

1 Like